Comparing Eurodollar Strips to Interest Rate Swaps
Publication: Journal of Derivatives
While interest rate swaps and strips of eurodollar futures can serve as substitutes for each other, use of futures necessarily fosters some degree of uncertainty with respect to the ex post results. Specifically, the practicalities of managing a strip of futures contracts designed to replicate an interest rate swap subjects the trader/hedger to 1) basis risk, and 2) an exposure relating to the dynamic transactional requirements of the futures position. Appropriate consideration of these aspects is a prerequisite for making ex ante relative value comparisons between swap rates and futures strip yields.
Those seeking to convert a floating-interest rate exposure to a fixed-rate, or vice versa, have two choices: interest rate swaps or eurodollar strip hedges. Conceptually, each solution will accomplish the same end, but they do so using different institutional market mechanisms. Because the two instruments offer the same ultimate service (i.e., converting fixed to floating rates, or vice versa), the pricing of the two alternative financial vehicles should be closely related.
Put more specifically, for interest rate swap contracts with maturities bounded by the length of the eurodollar futures strip, the quoted swap rate should correspond to the yield associated with the strip of eurodollar futures contracts that extends for the same period. Because the two alternatives are not perfect substitutes, however, some disparity of prices may be expected.
This article has two goals: 1) to provide a methodology for evaluating eurodollar strip yields, and 2) to demonstrate the process for determining the correct hedge ratios for eurodollar strip hedges designed as substitutes for interest rate swaps. Before embarking on these objectives, we describe the respective market mechanisms briefly.
I. SWAPS
Exhibit 1 summarizes the standard, “plain vanilla,” swap agreement. Here, two counterparties enter into a contract in which A calculates an interest rate expense obligation based on a floating-interest rate benchmark and B calculates an obligation based on a known, fixed rate.

The amount of the interest expense for which A is responsible will clearly rise in a rising rate environment and fall with declining rates. B’s obligation, by contrast, is constant, based on the notional amount specified by the swap agreement and the contractually determined fixed interest rate. The swap requires periodic interest payments equal to the difference between the two interest obligations (the net), paid by the party with the greater obligation to the party with the lesser obligation.1
Suppose A agrees to pay B based on the London Interbank Offered Rate (LIBOR) on three-month eurodollar deposits, and B agrees to pay A based on a fixed money market rate of 6%.2 Assume a notional amount of $100 million for the swap and quarterly interest settlements.
1 A parallel discussion could be offered in connection with interest revenues (an asset swap) as opposed to interest expenses (a liability swap).
2 The swap fixed rate typically is quoted as a spread over the yield on U.S. Treasury instruments (e.g., 20 basis points above five-year U.S. Treasuries). This practice allows quotations to be viable for an extended period.
With each fixing of LIBOR, a subsequent cash obligation is determined. If LIBOR were equal to 6% at the first rate-setting date, for example, no cash adjustment would be made by either party three months hence, on the settlement date. If LIBOR were 7%, counterparty A would pay B $25,000 ($100 million × 0.07 × 1/4 – $100 million × 0.06 × 1/4) on the settlement date. If LIBOR were 5%, counterparty B would pay A $25,000 ($100 million × 0.05 × 1/4 – $100 million × 0.06 × 1/4).3 This process continues for the term of the contract, following each reset of LIBOR.4
3 An alternative structure requires a settlement of the present value of the prospective cash adjustment, immediately following the setting of the variable interest rate.
4 As noted by Smith, Smithson, and Wilford, in Chapter 2 of Smith and Smithson [1990], swaps can be thought of as a series of forward contracts or forward rate agreements, where a series of long forwards would substitute for a long swap and short forwards for a short swap. In the case of a plain vanilla swap, however, all the forward rate benchmarks are equal. In the general case of a series of forward contracts, on the other hand, the respective forward rates would reflect implied forward rates dictated by the spot yield curve; and thus respective forward rates would likely be different for different reset dates.
If both A and B had no exposure to interest rates prior to the swap transaction, the swap would expose A to the risk of higher short-term rates and the opportunity of lower rates; B’s exposure would be the opposite. More likely, however, counterparties will use swaps to offset existing exposures. In the first case, the swap is being used as a speculative trading vehicle; in the second, it is being used as a hedge.
Three additional aspects of swaps warrant mention. First, as a principal-to-principal transaction, swaps can be tailored to meet the individual needs of the counterparties, which may reflect very specific timing and exposure characteristics. At the same time, some degree of standardization has evolved in the swaps market. As a consequence, participants can typically expect better markets (i.e., tighter bid/ask spreads and greater depth) when their transactions are of the more typical constructions, but somewhat less attractive pricing for more customized deals.
Second, swaps require separate settlements and documentation for each counterparty. Thus, the first deal with a new counterparty requires substantial preliminary work and legal attention. Subsequent deals, on the other hand, tend to be readily transacted. And, finally, and perhaps one of the more significant features of swaps, default risk is ever present, and the cost of non-performance may be considerable. With this last consideration in mind, swap counterparties have increasingly come to adopt collateral-adjustment practices designed to cover this exposure.
II. EURODOLLAR STRIPS
The eurodollar futures contract is a price-fixing mechanism that sets offered rates on three-month eurodollar time deposits, with the value date of the underlying deposit scheduled for the third Wednesday of March, June, September, or December. The precise rate in question is found simply by subtracting the futures price from 100. For example, a futures price of 95.00 reflects the capacity to lock up a 5% offered rate on the underlying three-month deposit. Given this convention, it should be clear that as interest rates rise, futures prices fall, and vice versa.
With the face amount of the eurodollar futures contract being $1 million, and with the underlying deposit having a maturity of three months, every basis point move in the futures price (yield) translates to a value of $25 ($1,000,000 × 0.0001 × 90/360). In general, movements in the eurodollar futures market are closely correlated with yield movements in the spot eurodollar time deposit market, although changes are not precisely equal over any given period.
The futures market participant can maintain either a long position, which profits from a rise in price and decline in yield, or a short position, which profits from a decline in price and rise in yield.5 In either case, the participant will be obligated to mark the contract to market on a daily basis and make daily cash settlements for any change in value, valued at $25 per basis point moved. Also, before any trade is initiated, market participants must post collateral or a “performance bond.”
5 Note that the terminology differs for eurodollar futures and off-exchange forward rate agreements. That is, the short futures, which profits from a rise in interest rates, corresponds to a long forward, and vice versa. Put another way, hedgers seeking to cover the risk of an interest rate increase could either short the eurodollar futures contract or execute a long forward contract on the rate.
A key benefit of this mark-to-market requirement and the initial performance bond is that the structure virtually eliminates credit risk or exposure to counterparty default.
The mark-to-market obligation can be terminated at any time by simply trading out of the position (i.e., making the opposite transaction to the initial trade). Upon expiration of the contract, however, any participant still maintaining an open position makes a final mark-to-market adjustment, and then the contract expires.
The final settlement price is based on an average interest rate derived from a survey of London bankers who report their perceptions of the cash market three-month offered rate to the Chicago Mercantile Exchange. This survey is undertaken two London business days before the third Wednesday of the contract month (i.e., on the trade date for a spot eurodollar deposit with a settlement date of the third Wednesday). Thus, the contract is said to be “cash-settled” with no allowance or capacity for a physical delivery process. Strips of eurodollar futures are simply the coordinated purchase or sale of a series of futures contracts with successive expiration dates. The objective is to lock up a yield for a period or term equal to the length of the strip.
For example, a strip consisting of contracts with four successive expirations would lock up a one-year term rate (for a one-year period beginning at the value date of the first contract in the strip); eight successive contracts would fix a two-year rate; and so on. As is the case with swaps, futures strips may be used to take on additional interest rate risk in the hope of making trading profits, or as an offset or hedge to an existing exposure.
III. CALCULATING STRIP YIELDS
The comparison of eurodollar strip rates to interest rate swap rates requires a four-step process, as follows:
1. Identify all prospective swap rate-setting dates and related maturities.
2. For each such rate-setting date, identify the appropriate futures contracts that would be used for hedging that specific exposure.
3. Depending on the relevant futures prices for each rate-setting date, determine the expected cash flow obligation that would result by hedging with appropriately structured futures hedges.
4. Calculate the internal rate of return, reflecting the projected stream of expected cash flow obligations.
Using price data from Exhibit 2, Exhibit 3 shows sample calculations where strips are constructed in an effort to synthesize spot interest rate swaps with an initial value date of 11/5/93. Interest settlements are assumed to be scheduled semiannually, with the first interest rate exposure occurring six months after the origination of the swap.
A spot seven-year swap with semiannual cash adjustments, for instance, has fourteen independent rate-setting dates. The first setting, and thus the initial cash flow obligation, is determined with the onset of the swap, leaving thirteen forthcoming discrete occasions of interest rate exposure.
Note in Exhibit 3, that given an initial spot value date of 11/5/93, the first reset is on the value date of 5/5/94; subsequent value dates fall on the fifth of November and May through the term of the hedge. Futures hedge rates for all exposures are calculated using the futures prices of the two futures contracts that immediately follow the hedge value dates.6
For example, for a hedge value date of 5/5/94, the June-94 and September-94 futures are the appropriate pair. The synthetic coupon (Ri) is the six-month money market yield associated with a given pair of futures, calculated as follows.7
6 Two-quarter strips rates are used because they are expected to correlate more closely with six-month interest rates than rates associated with any single contract.
7 While Equation (1) allocates equal weight to the component futures contracts, some users might prefer differential weighting. Moreover, while this specification compounds the two respective futures rates, an alternative approach might simply use the average. No universal standard appears to be in effect.
To solve for R1, the first synthetic coupon, relating to the 5/5/94 value date, requires the inputs:

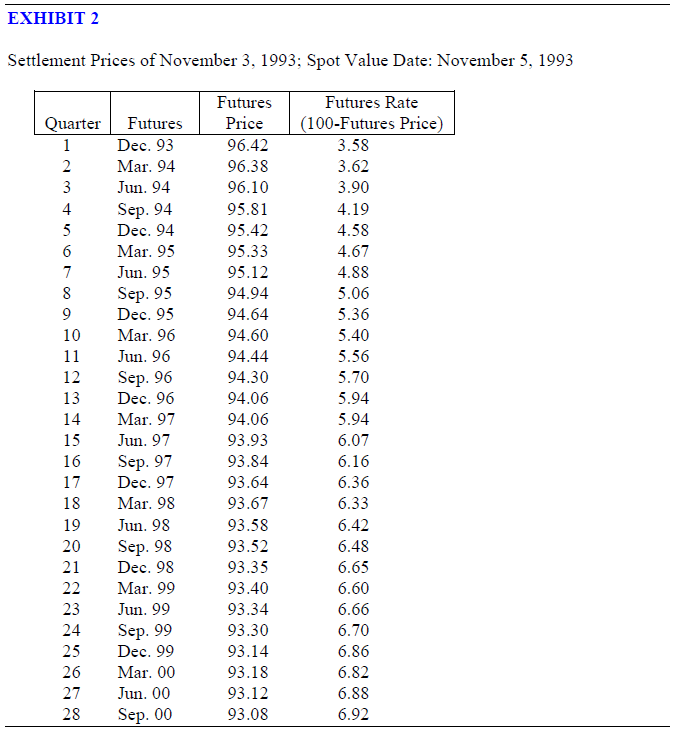
Settlement Prices of November 3, 1993; Spot Value Date: November 5, 1993
The fact that the hedge value date and the value date of the first futures contract in each hedge pair (i.e., the “lead” contract) are not generally coincident may cause the hedger to expect that the synthetic coupon rate will differ from spot six-month LIBOR upon the rate-setting date. For instance, differences might be anticipated because of some expectation that yield curves will exhibit a predominant shape (either upward-sloping or inverted) over the term of the hedge, or because of the presence of some expected liquidity premium. This difference — whatever the source — will directly modify the outcome, basis point for basis point.
The hedger, then, must make a best guess as to the magnitude of the average size of this non-convergence difference over the life of the hedge, or, alternatively, make some maximum/minimum estimates to generate best-case/worst-case potential results. The rationale for these adjustments may be best understood by analogy.
Consider the case of a hedger exposed to ninety-day LIBOR, on a $1 million exposure scheduled for a value date on the third Wednesday of a quarterly month. In other words, consider an exposure equal to the precise underlying instrument of a given eurodollar futures contract. Using the eurodollar futures to hedge this exposure results in an ex post effective rate equal to the rate reflected by the futures contract at the onset of the hedge. That is, irrespective of where LIBOR ultimately goes, an initial futures trade of, say, 95.00 will produce a post-hedge outcome of a 5% money market yield. If the timing of this exposure is such that the reset date precedes the futures expiration, however, and therefore the futures rate does not fully converge to the spot LIBOR, the resulting ex post outcome will differ from the initial futures rate by the amount of the non-convergence.
For example, assume the hedger initiates a hedge by selling one futures contract at a price of 95.00. Then, when the rate-setting date arrives, suppose LIBOR is 3% while the futures price is 96.90. In this case, the futures contract reflects an interest rate for the futures contract that is 10 basis points higher than spot (3.10% versus 3%). The interest on the ninety-day deposit (based on the 3% spot rate) is $7,500, while the futures generates a 190-basis point move, or a loss of $4,750.
Consolidating the futures loss with the cash interest expense would produce a net interest value of $12,250, equivalent to the ex post money market yield of 4.90% — 10 basis points below the futures rate at the start of the hedge. Again, the ex post result is the initial futures rate adjusted for the basis conditions at the time of the hedge liquidation. A downward adjustment made to the synthetic coupon calculations reflects an implicit assumption that spot six-month LIBOR will be less than the liquidation value of Ri on the rate-setting dates. This condition will typically hold when upward-sloping yield curves are present. When inverted yield curves are expected, upward adjustments of the original Ri calculations would be justified.
Determining the magnitudes of these adjustments necessarily requires some degree of judgment, but a reasonable approach might be to start by measuring this non-convergence differential over time, limiting the assessment to those data where the time between the hedge value dates and the futures value dates is comparable to the typical life of the hedge. For example, if the timing of the lead futures value date follows the hedge value dates by about a month, the analyst should assemble historical time series data showing the extent of this past non-convergence, restricting data to observations taken one month prior to futures expirations.
The specific adjustments in Exhibit 3 reflect an assumption of upward-sloping yield curve conditions prevailing on rate-setting days, where the size of the adjustment is directly related to the length of time between the relevant hedge value date and the next subsequent futures value date. As a consequence, a larger (shorter) time differential justifies a bigger (smaller) adjustment. For these calculations the assumed adjustment is 0.1 basis points per day, downward.
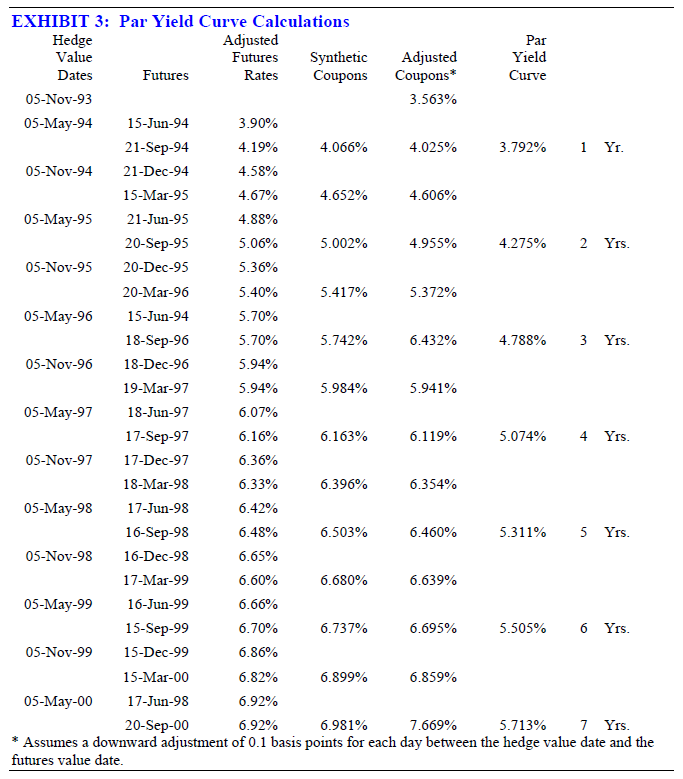
To illustrate, consider the adjustment associated with the 5/5/94 exposure. From 5/5/94 to 6/15/94 (the futures value date) is a period of forty-one days. The product of 41 × 0.1 = 4.1, or about 4 basis points. Thus the adjusted synthetic coupon corresponding to the rates on the June- and September-94 futures contracts is 4.066 – 0.041 = 4.025%, as shown in Exhibit 3. Over the entire seven-year span, because of some small differences in the timing between hedge value dates and the lead futures value dates, these adjustments range from four to five basis points.
Finally, the determination of the par yield curve simply reflects the internal rate of return associated with the stream of cash flows that arises from the original spot variable interest rate and all subsequent adjusted coupons, for the various maturities shown in Exhibit 3.
IV. SIZING THE HEDGE
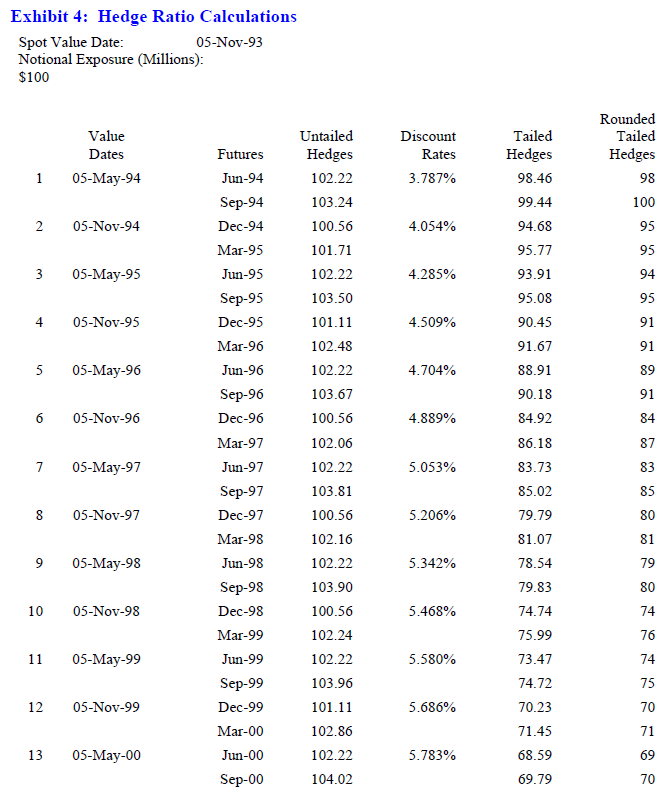
In order to realize the projected returns dictated by the strip yield calculations, in addition to assessing the basis adjustment properly (i.e., selecting the appropriate magnitude for the adjustment of the synthetic coupon), a hedge must be implemented using the correct number of futures contracts for each of the respective exposures. These results are shown in Exhibit 4 for a $100 million swap, again assuming semiannual settlements.
Conceptually, it may be helpful to view each six-month exposure as if it were composed of two three-month segments. The problem then can be viewed as hedging a series of exposures, each with two parts: $100 million for the initial three months, and $100 million plus interest for the subsequent three months. For simplicity, the calculation assumes the second component of the exposure is equal to
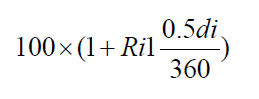
where Ri1 is the rate on the lead futures contract for the ith exposure, and di is the number of days between the ith value date and the subsequent hedge value date.
For instance, in the case of the first exposure of 5/5/94, given the capacity to lock up a three-month rate of 3.90% (from the June-94 contract) and 184 days between 5/5/94 and 11/5/94, the second component exposure becomes 100(1 + 0.039 × 92/360) = $101 million. Thus, for the June-94 contract we use an exposure of $100 million, and for the September-94 contract we use $101 million. Then, the value of a basis point (BPVi) for each component exposure (EXPi) is found by the formula:8

8 As in Equation (1), no universally accepted methodology applies to this basis-point value calculation. Discrepancies due to alternative day-counts, however, are inconsequential compared to the inherent rounding difficulties in employing whole numbers of futures contracts.
To illustrate, for the June-94 futures, BPV is $100 million × 0.0001 × 92/360 = $2,555.55; for the September-94 futures, BPV is $101 million × 0.0001 × 92/360 = $2,581.11. Given a $25 value of a basis point for the eurodollar futures contract, the untailed hedge is simply the above BPVs divided by $25. For the June-94 and September-94 contracts, these calculations dictate 102.22 and 103.24 contracts, respectively. These and all subsequent untailed hedge ratios are shown in Exhibit 4.
This interim result has the limitation that it ignores the timing difference between the effects of an interest rate change on the exposure and the cash flow results of the same change in rates on the futures hedge. As illustrated in Exhibit 5, which relates to the interest flow to be paid on 11/5/97, the former effects are not realized until the maturity date associated with the exposure when actual interest flows are paid and received, while the latter start immediately and accrue daily.
To adjust for this timing mismatch, the proper hedge calculation should offset the present value of the exposure’s basis point value, where the discount rate and the discounting term should reflect the point on the yield curve associated with the interest flow date — 11/5/97, in the case of the 5/5/97 rate reset, as an example. This adjustment is known as “tailing” the hedge (see Figlewski, Landskroner, and Silber [1991]).

The revised hedge ratios need to be proportional to untailed hedges, where the present value factor is 1/(1 + Rdis)T. In this expression, Rdis is the interest rate used in discounting, and T is the number of periods between the initial spot value date and exposure interest flow.
The discount rates shown in Exhibit 4 incorporate the spot eurodollar offered rate appropriate for the period from 11/5/93 to 12/15/93 (i.e., to the first futures value date), commonly designated as the stub rate, which is then compounded with each successive futures rate. These various rates are shown in Exhibit 6 in column (2). Column (3) shows the single-period effect of investing/funding $1 at the given yield for the associated period. The cumulative product of these terms in column (4), therefore, shows how $1 compounds over time.
The bond-equivalent yield (BEY) is simply the discount factor that relates the future values shown in column (4) to a present value of $1. Discount rates shown are expressed as zero-coupon bond-equivalent yields, assuming semiannual compounding.
This process generates zero-coupon rates appropriate for maturities that correspond to all the futures value dates in column (6). Discount rates that are required for the untailed hedge ratio calculations, however, should correspond to the exposure interest flow dates. These discount rates are found simply by linear interpolation.
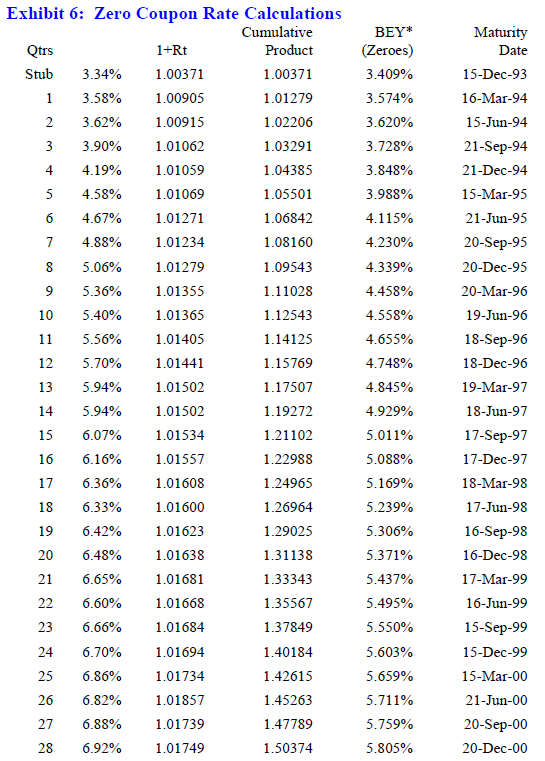
For example, the first discount rate given in Exhibit 4 (3.787%) relates to an interest flow date of 11/5/94. This rate is the result of interpolating rates associated with 9/21/94 and 12/21/94 (given in Exhibit 6), which are 3.728% and 3.848%, respectively. Given this discount rate of 3.787% and an exposure interest flow date of 11/5/94 (i.e., reflecting a maturity of exactly two semiannual periods), the present value factor required for both the June-94 and September-94 hedge ratios is 1/(1 + 0.03787/2)2 = 0.9632.
Tailed hedge ratios for each pair of futures are found simply by multiplying the untailed hedges by the appropriate factor. For the June-94 and September-94 futures, the results are 102.22 × 0.9632 = 98.46, and 103.24 × 0.9632 = 99.44, respectively. It should be clear that the magnitude of the tail itself (i.e., the difference between the untailed hedge ratio and the tailed hedge ratio) grows directly with the span of the hedge period. For example, again referring to Exhibit 4, the tail for the June-94 futures is only four contracts (102 – 98), but the tail for the September-2000 futures is thirty-four contracts (104 – 70).
From another perspective, failure to tail a hedge may be thought of as failing to account for the interest revenue that would necessarily result from investing hedge profits, or the expense or opportunity cost associated with hedge losses from the date they are received (or paid out) until the date of the cash flow they are meant to hedge. To adjust for these consequences appropriately, the hedger would need to “underhedge” by the amount of the tail.
Maintaining a correctly tailed hedge requires a dynamic adjustment as interest rates change or as time goes by. Ultimately, the tailed hedge will approach the untailed hedge requirement, as the present value factor approaches unity. Stated in another way, dynamic hedge adjustments are required because the difference between the future value of a basis point and the present value of a basis point erodes as the hedge value date approaches. Note that “rounded tailed hedges” offered in the far right column of Exhibit 4 are calculated so as to round the cumulative hedge requirements. That is, the 99.44 contracts required for the September-94 contract round up to 100 futures because of the rounding down of the June-94 contract.
V. EX POST RESULTS
Assuming that a eurodollar strip hedge is composed as prescribed, does this mean that the targeted outcome is certain to be realized? Frankly, it does not. Two considerations could work to distort the outcomes.
First, as mentioned earlier, the initial rate calculations impose an assumption about the difference between six-month LIBORs and the rates generated from the associated pair of eurodollar futures. For instance, Exhibit 3 reflects the assumption that on 11/5/94, the December and March strip will be liquidated with an associated synthetic coupon rate about four basis points higher than the then-prevailing six-month LIBOR.9 The ex post result will differ from the ex ante expectation if this assumption proves to be invalid.
9 This difference of 12 basis points reflects the difference between 4.066% and 3.943%.
Larger differences between the Ris and six-month LIBORs will foster a lower effective interest rate realized from the hedge, compared to initial expectations, and vice versa. If these errors turn out to be offsetting over the life of all the individual cash flow hedges, the targeted outcomes would again result, but if the original estimates are systematically off, so too would be the ultimate outcomes.
The second source of errors deals with the effect of volatility of the yield curve and associated adjustments in hedge ratios. Suppose that some initial long hedge of X contracts is implemented to lock up a deferred rate of return on a prospective asset purchase, and immediately after hedging this exposure, the yield curve shifts upward, raising all the discount rates used in determining the present values of the basis point exposures. In turn, the requisite number of futures contracts in the tailed hedges declines, causing the hedger to sell contracts in order to remain properly hedged. If the discount rates then fall back to their original values, the adjustments would have to be reversed.
Thus, the rate movement forces a sale of contracts and then a subsequent repurchase. As the associated futures prices would likely move in concert with the movement of the discount rates, these hedge adjustments unfortunately would force the hedger to sell at a lower price and then buy back at a higher price. In other words, hedge adjustments needed to maintain an appropriately tailed hedge typically will foster losses for the long futures hedger.
Conversely, this tailing adjustment process works to the benefit of the short futures hedger.10 Put yet another way, these adjustments ultimately work to lower the ex post strip yield from the original ex ante calculation, whether the hedge is long or short.
To give some indication of the magnitude of this effect, consider the overall hedge for the synthetic seven-year swap shown in Exhibit 4. At origination, this hedge requires a total of 2,177 futures.
10 A similar issue relates to the use of eurodollar futures for hedging bonds or instruments that exhibit price convexity. See Flesaker [1993]. Burghardt et al. [1991] also consider a related effect when comparing eurodollar futures to implied forwards.
Assume a hedge adjustment rule that requires altering the hedge following an average rate move of 10 basis points per contract. Under such a rule, an immediate decline of all futures prices by 0.10 would dictate increasing the hedge by seven contracts. A rate reversal would then produce an effect of $1,750 (seven contracts × 10 basis points × $25 per basis point) — to the benefit of the short hedger and the detriment of the long hedger. As time goes on, the overall hedge requirement declines with the passing of reset hedge dates; and thus the magnitude of this adjustment effect also diminishes.
Relative to the overall exposure, these individual hedge adjustments produce inconsequential effects. The ultimate consequence of these adjustments, however, is cumulative over time. More frequent and larger adjustments (i.e., greater volatility) will create larger effects, and vice versa; the size of the combined effects will be completely determined only after all the individual hedges are liquidated.
To the extent that market participants recognize and value this prospective hedge adjustment effect, it should be reflected by a difference between quoted swap rates and calculated strip yields. Put another way, market participants should be indifferent between entering into a swap at a given rate and trading a futures strip valued at a somewhat higher yield, ex ante.
The difference between the initial strip yield (adjusted for expected basis liquidation conditions) and the prevailing swap yield should then be a measure of the market’s assessment of the value of these dynamic hedge effects and/or its view of prospective interest rate volatility. This valuation is complicated, however, because the basis liquidation adjustment is largely subjective.
VII. CONCLUDING REMARKS
This article analyzes the construction of eurodollar strip hedges designed as alternatives to interest rate swaps, highlighting the practicalities of hedge construction. In particular, the article focuses on two aspects of futures hedging that foster uncertainty: 1) that interest rate-resetting days typically do not coincide with futures expirations, and 2) that the dynamic process of maintaining a correctly sized futures hedge is advantageous (disadvantageous) to the short (long) hedger.
Before comparing prices of interest rate swaps to eurodollar futures strips, estimates must be made as to the likely magnitudes of these effects. Unfortunately, the ex post outcome of the futures strip cannot be fully determined until the final rate-setting date and the liquidation of the last component futures contracts. Only then can the original value judgment be validated.
Of course, other conditions besides price may be overriding in the choice between swaps and futures strips, such as concerns about credit risk, liquidity, and institutional relationships. All these aspects warrant consideration in identification of the more attractive instrument.
References
Burghardt, G., T. Belton, M. Lane, G. Luce, and R. McVey. Eurodollar Futures and Options: Controlling Money Market Risk. Chicago: Probus Publishing Company, 1991.
Figlewski, S., Y. Landskroner, and W. Silber. “Tailing the Hedge: Why and How.” Journal of Futures Markets, Vol. 11, No. 2 (1991), pp. 201-212.
Flesaker, B. “Arbitrage Free Pricing of Interest Rate Futures and Forward Contracts.” Journal of Futures Markets, Vol. 13, No. 1 (1993), pp. 77-91.
Macfarlane, J., D. Ross, and J. Showers. “The Interest Rate Swap Market: Yield Mathematics, Terminology and Conventions.” Salomon Brothers Inc, undated.
Smith, C., and C. Smithson, eds. The Handbook of Financial Engineering. New York: Harper & Row, 1990.
“Using Interest Rate Futures and Options.” Chicago Mercantile Exchange, undated
HedgeStar Media Contact
Megan Roth, Marketing Manager
Office: 952-746-6056
Email: mroth@hedgestar.com

